0%

计算掉落概率

Posted on Edited on In

计算掉落概率

在游戏中经常遇到按一定的掉落概率来随机掉落指定物品的情况，例如按照：钻石10%，金币20%，银币50%，饰品10%，装备10% 来计算掉落物品的类型。

通常的做法是将物品掉落概率（或者权重）变成一个离散的列表，随后产生一个随机数，再在列表中找到第一个大于该随机数的数，这个数对应的下标也就是对应的物品类型。

对应前面的例子，第一步会构建一个列表 [0.1, 0.3, 0.8, 0.9, 1.0] ；第二步生成一个随机数 0.56（假设）；第三步在列表中查找到第一个大于 0.56 的数是 0.8，下标为 2，此时掉落物品应该为银币。

这种算法比较直观，理解和实现起来也比较容易。很多时候甚至都不需要预先构建列表，而是每次累加概率直到找打大于随机数的那个数的下标。但是运用这个算法的时候，第三步我们往往使用的是顺序查找，这在掉落类型较多的时候确实不怎么好。当然大多数情况类型的种类并不是一个很大的数，所以其实也没有影响。（后面实现时候采用二分查找）

在上周的技术交流会时，同事提到了一个掉落概率算法 Alias Method，这个算法比较有意思，实现的很巧妙。算法的论文在这里：《Darts, Dice, and Coins: Sampling from a Discrete Distribution》

(以下引用自 《抽奖概率-三种算法》)
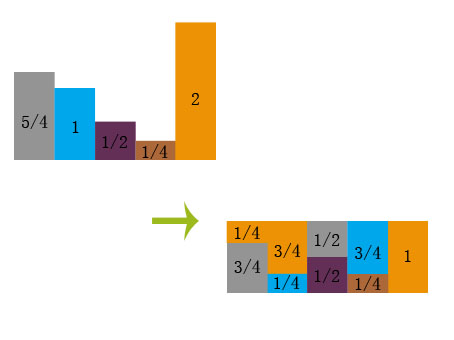
Alias Method 算法大概是这么做的：把 N 种可能性拼装成一个方形（整体），分成 N 列，每列高度为 1 且最多 2 种可能性。可能性抽象为某种颜色，即每列最多有 2 种颜色，且第 n 列中必有第 n 种可能性，这里将第 n 种可能性称为原色。 想象抛出一个硬币，会落在其中一列，并且是落在列上的一种颜色。这样就得到两个数组：一个记录落在原色的概率是多少，记为 Prob 数组，另一个记录列上非原色的颜色名称，记为 Alias 数组，若该列只有原色则记为 null。

为了直接用网上的图片，我把前面例子的掉落概率依次改为 1/4, 1/5, 1/10, 1/20, 2/5。

由上图方形可得到两个数组： Prob: [3/4, 1/4, 1/2, 1/4, 1] Alias: [4, 4, 0, 1, null] (记录非原色的下标)。之后就根据 Prob 和 Alias 获取其中一个物品，随机产生一列 C，再随机产生一个数 R，通过与Prob[C] 比较，R 较大则返回 C，反之返回 Alias[C]。

Alias Method 算法

算法论文中已经有了一个 java 的版本，这里我就按照作者 java 实现 “翻译” 了 python 和 C# 版本。

python 版本
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
#!/usr/bin/env python
# -*- coding: utf-8 -*-

from __future__ import division

import random

class AliasMethod4Sample(object):

    def __init__(self, probabilities_or_weights):
        assert probabilities_or_weights is not None
        assert isinstance(probabilities_or_weights, (list, tuple))

        self._probabilities_or_weights = probabilities_or_weights
        self._alias = [None] * len(probabilities_or_weights)

        total = sum(probabilities_or_weights)
        self._probabilities = map(lambda x: x/total, probabilities_or_weights)

        self.__preprocess()

    @property
    def probabilities_or_weights(self):
        return tuple(self._probabilities_or_weights)

    @property
    def probabilities(self):
        return tuple(self._probabilities)

    @property
    def alias(self):
        return tuple(self._alias)

    def __preprocess(self):
        average = 1.0 / len(self._probabilities)
        small = []
        large = []

        for index, val in enumerate(self._probabilities):
            if val >= average:
                large.append(index)
            else:
                small.append(index)

        while small and large:
            less = small.pop()
            more = large.pop()

            self._probabilities[more] = self._probabilities[more] + self._probabilities[less] - average
            # 为已经预处理好的颜色设置 `原色` 的概率和对应的 `非原色`
            self._probabilities[less] = self._probabilities[less] * len(self._probabilities)
            self._alias[less] = more

            if self._probabilities[more] >= average:
                large.append(more)
            else:
                small.append(more)

        while small:
            self._probabilities[small.pop()] = 1.0

        while large:
            self._probabilities[large.pop()] = 1.0

    def next(self):
        current_index = random.randint(0, len(self._probabilities) - 1)
        current_number = random.random()

        if current_number < self._probabilities[current_index]:
            return current_index
        else:
            return self._alias[current_index]
C# 版本
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
public class AliasMethod4Sample
    {
        private readonly Random _random = new Random();

        public Double[] ProbabilitiesOrWeights { get; private set; }

        public Int32[] Alias { get; private set; }

        public Double[] Probabilities { get; private set; }

        public AliasMethod4Sample(ICollection<Double> probabilitiesOrWeights)
        {
            if (probabilitiesOrWeights == null)
            {
                throw new ArgumentNullException("probabilitiesOrWeights");
            }

            if (probabilitiesOrWeights.Count == 0)
            {
                throw new ArgumentException("probabilitiesOrWeights is empty.", "probabilitiesOrWeights");
            }

            ProbabilitiesOrWeights = probabilitiesOrWeights.ToArray();
            Alias = new Int32[ProbabilitiesOrWeights.Length];

            var sum = ProbabilitiesOrWeights.Sum();
            Probabilities = ProbabilitiesOrWeights.Select(x => x/sum).ToArray();

            Init();
        }

        public Int32 Next()
        {
            var index = _random.Next(0, Probabilities.Length);
            var val = _random.NextDouble();

            return val < Probabilities[index] ? index : Alias[index];
        }

        private void Init()
        {
            var average = 1.0/Probabilities.Length;
            var small = new Queue<Int32>();
            var large = new Queue<Int32>();

            for (var i = 0; i < Probabilities.Length; i++)
            {
                if (Probabilities[i] >= average)
                {
                    large.Enqueue(i);
                }
                else
                {
                    small.Enqueue(i);
                }
            }

            while (small.Count > 0 && large.Count > 0)
            {
                var less = small.Dequeue();
                var more = large.Dequeue();

                Probabilities[more] = Probabilities[more] + Probabilities[less] - average;
                Probabilities[less] = Probabilities[less]*Probabilities.Length;
                Alias[less] = more;

                if (Probabilities[more] >= average)
                {
                    large.Enqueue(more);
                }
                else
                {
                    small.Enqueue(more);
                }
            }

            while (large.Count > 0)
            {
                Probabilities[large.Dequeue()] = 1.0;
            }

            while (small.Count> 0)
            {
                Probabilities[small.Dequeue()] = 1.0;
            }
        }
    }

常用的离散算法

常用的离散算法，第三步改为二分查找。

python 版本
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#!/usr/bin/env python
# -*- coding: utf-8 -*-

from __future__ import division

import random
import bisect


class DiscreteMethod4Sample(object):

    def __init__(self, probabilities_or_weights):
        assert probabilities_or_weights is not None
        assert isinstance(probabilities_or_weights, (list, tuple))

        total = sum(probabilities_or_weights)
        discrete_table = []
        for pw in probabilities_or_weights:
            if discrete_table:
                discrete_table.append((discrete_table[-1] + pw)/total) 
            else:
                discrete_table.append(pw/total)

        self._discrete_table = discrete_table
        self._probabilities_or_weights = probabilities_or_weights

    @property
    def discrete_table(self):
        return tuple(self._discrete_table)

    @property
    def probabilities_or_weights(self):
        return tuple(self._probabilities_or_weights)

    def next(self):
        current_probability = random.random()
        return bisect.bisect_right(self._discrete_table, current_probability)
C# 版本
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
public class DiscreteMethod4Sample
    {
        private readonly Random _random = new Random();
        private readonly List<Double> _discreteTable;

        public Double[] ProbabilitiesOrWeights { get; private set; }

        public Double[] DiscreteTable
        {
            get
            {
                return _discreteTable.ToArray();
            }
        }

        public DiscreteMethod4Sample(ICollection<Double> probabilitiesOrWeights)
        {
            if (probabilitiesOrWeights == null)
            {
                throw new ArgumentNullException("probabilitiesOrWeights");
            }

            if (probabilitiesOrWeights.Count == 0)
            {
                throw new ArgumentException("probabilitiesOrWeights is empty.", "probabilitiesOrWeights");
            }


            var rawProbabilitiesOrWeights = probabilitiesOrWeights.ToArray();
            var discreteTable = new Double[probabilitiesOrWeights.Count];

            discreteTable[0] = rawProbabilitiesOrWeights[0];
            for (var i = 1; i < rawProbabilitiesOrWeights.Length; i++)
            {
                discreteTable[i] = discreteTable[i - 1] + rawProbabilitiesOrWeights[i];
            }

            var total = rawProbabilitiesOrWeights.Sum();
            ProbabilitiesOrWeights = rawProbabilitiesOrWeights;
            _discreteTable = discreteTable.Select(x => x/total).ToList();
        }

        public Int32 Next()
        {
            var index = _discreteTable.BinarySearch(_random.NextDouble());
            return index < 0 ? ~index : index;
        }
    }